CYLINDERS

Aim: How do we calculate surface area of cylinders?

By using the formula  (.-.)!!

What is a cylinder?A cylinder is a solid geometric figure with straight parallel sides and
a circular or oval section.

As you can see a cylinder has two circles as a base, and the round body is actually a rectangle.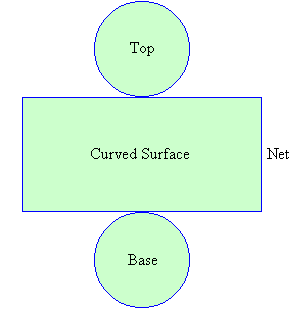








How can we solve for he surface area of a cylinder?

Onw way is by calculating the area of the bases which is (r squared times pii), and adding the area of the bases to the area of the rectangle which is length times width.

Example:



The radius is 6 inches. You have to multiply the radius to the square.
Which is 36 inches cubed. Then, multiply times pii,which going to  be 113.09 inches squared.
Then, you add that to the area of the rectangle which is 300 inches squared because the height is 25 inches and the diameter gives you the width which is 12 inches because the diameter is twice the rdaius and the radius is 6 inches so 6 * 2  equals twelve. Finally, you add 300 inches squared with 113.09 squared, which gives you 413.09 inches cubed.

What is the formula?

The formula for the surface area is the following:



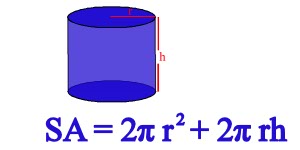
All you have to do is substitue the number with radius and you will get the surface area-.-

Example: The radius of a circle is equal to 7. And height equals to 15

SA= 2pii r squared + 2 pii r h.
SA=2 pii 7 squared +2 pii 7 *15
SA= 2 pii 49 +2 pii *105
SA= 98 pii + 210 pii
SA= 308 pii
SA= 967.61


                                                Try it on your own!!


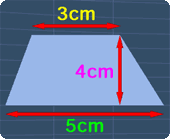
What is the surface area for the given cylinder??


ALL PICTURES FROM GOOGLE.

Aim: How do we solve compound area problems?

You need to find the area of the first figure and add the sum to the area of the second figure.

Example:



As you can see this figure can be divided into two rectangles. First step you divide the figure in to two figure or more if needed.
In this figure, we have two rectangles. To find the area of a rectangle you need to multiply the length and the width.
For the rectangle on the left side, the height is 9 cm. We need to find the width. As you can see on the top of the rectangle on the right there is a measurement of 6 cm. On the base there is a mesurement of 10 cm . You subtract 10 -6 which gives you . The next step is that if we cut the rectangle all the way from the 6 cm lines the height will not be 9 cm. On the right side there is a line that says 2 cm you have to subtract 9 from 2 which will give you seven.
Then, you multiply 4*7 which will give you a product of 28cm cubed.

For the second rectangle, we already got the measurements for it the width is 2cm and the length is 10 cm. 10cm * 2 cm equals to 20 cm squared.
Lastly you add the areas of the two figure and you are left with 28 cm cubed plus 20 cm cubed and you get a sum of 48 cm cubed, and that is your area.



                                                   Try it on your own!!


What is the area of this figure?




All info. from my brain and pics. from google.com.

Aim: How do we find the area of circles?

You can find areas of circles by using the formula which is going to be tought through this lesson.:)

Circle
What is the formula for the area of a circle?



Pii times the radius to the cube(square).

 Here is an exapmle:

A circle has a radius of 22. First you are going to ssquare the radius which will give you 484!!
After that you multiply by pii. Then you multiply by pii. You`re final product is 1,520.53.


What about if they give you the diameter and not the radius?
All you need to do is divide the diameter by 2 since the diameter is twice the size of the radius.


Here is an example,



You divide 38 cm by 2. Which will give you 19.
Then, you multiply by pii. Which will then give you a product of 59.69.

How about if they give you the circumference?
 First of all in order to find the circumference of a circle you need to multiply diameter times pii.
In order to find the area of a circle you need the radius. Therefore, you divide the product by two and you will get the radius. From there, you move on and multiply by pii.

Here is an example:



This circle has a diameter of 18 and when you multiply by pii you get 14.85. You divide the diameter by two which gives you 9. Nine cubed equals to 81. Then you multiply by pii and you get a product of 254.46.


                                                 Try it on your own!!

What is the area of of a circle which has a radius of 234 cm? Hmmmmmm?

All info. from my brain and pics. from google.com

Aim: How do we find the areas of parallelograms,kites, and trapezoids?

By using their formulas.

Parallelograms

How can we find the area of a parallelogram?

Well, one easy way is by using the formula.

The formula for a parallelogram is the same formula for a rectangle!!!!

Because if slice out one of the slanted edges of the parallelogram and put it togeether with the other side you get arectangle.

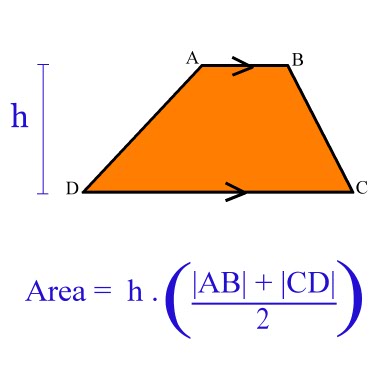
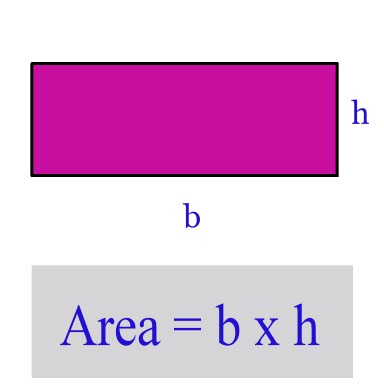
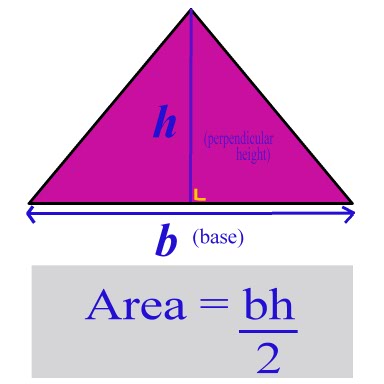
 Equals to area of


Recall: What was the formula for rectangles?
Base *hieght = Area

So if the parallelogram has a height of 7.6 in. and a base of 6in. the area is
going to be 45.6 cm cubed.

Try it on your own!!

What is the area of the parallelogram below?



Kites


\

Just follow these steps identify the d1  and d2.




Try it on your own!!



Trapezoids

A trapezoid is a quadrilateral with on pair of parallel lines.

The formula for a trapezoid is the following;



AB =base 1 DC = base 2.

Area= height*base 1 + base2 / 2.


Try it on your own!!




What is the area of the figure above?

All info. from my brain and  images from goolgle.com

Aim: How do we calculate the areas of rectangles and triangles?
You can calculate the areas of rectangles and triangles by using their formulas.

First of all what is the definition of area?

Area means the amountof surface area a figure takes up.

We sre going to learn how to find the area for traingle and rectangles.

Rectangles

There are two ways to find the area of a rectangle.

The first way is by counting the square units.
1 box is one square unit therefore the area of the rectangle below is 8 square units.



Another way is by using the formula which is



HERE IS A GREAT EXAMPLE:







All you have to do is multoply the length and the width. In this exapmle, the length is 5 inches and the width is 3 inches so the area is going to be 15 inches to the cube.

HINT: ALWAYS MULTIPLY THE MEASUREMENT MEANING INCHES CENTIMETERS AND ETC.!!

Try it on your own!!

Arectangle has width of 10 cm and a length of 18 cm what is the area of the rectangle?

Also, if a problem gives you the area and asks you for the length or width all you need to do is divide the two numbers.

For example, if a rectangle has an area of 24 cm squared and they give you the length whivh is 6 cm. All you have to do is divide the two numbers and your supposed to get 4 cm.


Triangles

Traingles also can be measured by square units and also by usong the formula.

Here is an examplke using square units.
Follow the same steps just count the little squares.






Using the first triangle count how many square unbits it has.

Answer:aprox. 33 square units

What is the formula for finding the area of a triangle?





Base times height divided by two.

Here is an example:



The height is 4 ft. in this figure and the base was 6 ft so 6 ft.*4ft.= 24 ft./2 =12 ft.

By the what if you get confused and do not know what measurment is the height the answer will be the one with the right angle on the top or bottom.



Try it on your own:
What is the area of the triangle below.




All info from my brain. and images fro google and my drawing in paint!!

Aim: How can we identify compound loci?

First of all what is compound loci?
Compound loci is when a problem contains two or more locus condition within one problem.

Here is an easy way of solving compund loci problems:

Steps:
1.  Draw a diagram showing the given information in the problem.  
2.  Read carefully to determine one of the needed conditions.  (Look for the possibility of the words "AND" or "AND ALSO" separating the conditions.)
3.  Plot the first locus condition.  If you do not see one of the locus theorems at work in the problem, locate one point that satisfies the needed condition and plot it on your diagram.  Then locate several additional points that satisfy the condition and plot them as well.  Plot enough points so that a pattern (a shape) is starting to appear, or until you remember the needed locus theorem for the problem. 
4.  Through these plotted points draw a dotted line to indicate the locus (or path) of the points.
An example would be the following:
What is the coordinates of points two units from the origin and what are the points that are 1 unit from the y axis.
The answer is 4 because the locus of points from the origin will be a circle and the lines from the y axis are y=-1 and y=1 so there are four points that satisfy both.
                                                    

QUESTION:

What are the locus of points 3 units from the origin and
locus of points 2 units to the right on the y-axis? Place an x on the points that satisfy both.

5.  Repeat steps 2-4 for the second locus condition.

6.  Where the dotted lines intersect will be the points which satisfy both conditions.  These points of intersection will be the answer to the compound locus problem.

loci

Aim: How do we find locus of points?
By finding what satisfies the problem and inorder to do that here are some theorems I want to show you.

By following the different types of loci problems which are the following:\

A fixed distance from a point.

1.The locus of points at a fixed distance, d, from point P is a circle with the given point P as its center and d as its radius.

Hint: If you are ever asked to find the locus of points from a point it is always a circle!
2. The locus theorom number two.                                                                                                            

The locus of points at a fixed distance, d, from a line, l, is a pair of parallel lines d distance from l and on either side of l.

The locus of points equidistant from two lines is 1 line and they are always parallel.

3. The third theorem is the following:                                    

 

The locus of points equidistant from two points, P and Q, is the perpendicular bisector of the line segment determined by the two points.

This picture shows that all the points equidistant from two other points is a perpendiculsr bisector.

4. The fourth theorem is the following: this is an example from regents pre.org!!

 During your morning jog, you run down an alley between two buildings which are parallel to one another and are 20 feet apart.  Describe your path through the alley so that you are always the same distance from both buildings.

Answer:

To maintain an equal distance from each building, you must jog in a straight line parallel to the buildings and halfway between them.  In this problem, since the buildings are 20 feet apart, you will jog on a line 10 feet from each building. 

The locus of points equidistant from two parallel lines, l1 and l2 , is a line parallel to both l1 and  l2 and midway between them.

 5. The final theorem is the following:

The locus of points equidistant from two intersecting lines, l₁ and l₂, is a pair of bisectors that bisect the angles formed by l₁ and l₂ .

 In this picture line 1 and line 2 show all the possible points that are equidistant to the x and y axis which is the red dotted lines!!



Try it out!!
When he is not in the house, Fido is tied to a stake in the backyard.  His leash, attached to the stake, is 15 feet long.  When traveling at the end of his leash, what is the locus of Fido's path?

 ALL PICTURES ARE FROM REGENTSPREP.ORG i LUV U REGENTS PREP!!

Aim: How do we solve logic problems using conditionals?

By adding if and then.

Review: Put this in conditional form.

Where ever you have oxygen there is life.

Answer: If there is oxygen somewhere then there is life.

Put the statement in inverse form too!!

Converse:
When you are using converse I mean converse in math not actual converse you just switch
the hypothesis and the conclusion.

For exapmle:

If there is life then there is oxygen.
It then becomes If there is oxygen then there is life.

This is using inverse because it is adding not into it :)!!
Try it Out:
Today is Thursday.
Tomorrow is Saturday.

Contrapositive:
 In order to contrapositive a stament you have to negate (which is adding not) and switch.

For example:
If tomorrow is not Saturday then today is not Friday.

Try it out!!

If there is water and land turtles can live.

http://www.google.com/imgres?start=140&um=1&hl=en&sa=N&biw=819&bih=316&tbm=isch&tbnid=svFN0sDDGCYmxM:&imgrefurl=http://englishbunghole.blogspot.com/2011/03/conditionals_30.html&docid=owNrQ4SkrybiwM&imgurl=https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgOvkD2q3xKIjyq2bIYXVp0X_rNzgxUmhPFOKyFiLXVvWGRYKkWUxaUSkR30OUtKWk-c4aA3oK-8kuTfegpoliVXL2dfwYsgliSCF9FtBhyg_aE_ksTedLtYEYAkd14peUzJ7KJhkC0iJc/s1600/your-shoes.png&w=248&h=320&ei=VkhST9G-JKaN0QHnlYXwDQ&zoom=1&iact=hc&vpx=512&vpy=-58&dur=2605&hovh=255&hovw=198&tx=123&ty=248&sig=114741552484678553676&page=10&tbnh=114&tbnw=84&ndsp=14&ved=1t:429,r:3,s:140

Aim: What is a mathematical statement?

A mathematical statement is a statment you can reason to decide weteher something is true
or false.

You can tell this is false because pencils and pens do no have viruses.
I had the same problem!!

Example

Adjacent sides, are sides that are next to each other.  This is true because adjacent means
 next to.

Try it out!!
Judge wether these statements are true or false. Circle T for true or F for false.
 
Five plus five equals 10.                        Truth value: T or  F

Twenty times five equals 1,000,000       Truth value:  T or F

Absolute value is the distance from         Truth Value: T or F
 a certain number to 0.
-------------------------------------------------------------------------------------------------------------

Lunch period starts at 12:47 and ends at 1:29.

In order for a statement to be true while using and both parts must be true.

You can do the handout I gave you or do deltamath for extra credit.

When you are using or either one of the statements can be true or both can be true in order
for the statemnt to be true.

                                                   Conditionals

Conditionals are words to show cause and effect. The words we use are If and Then.

If my grades are higher then 95 in each class then I`ll get $100.

An example of how to put sentences in conditional form is the following:

When it rains. I get my Umbrella.

If it rains then she gets her umbrella.
You just add if infront of the sentence and then for the result.

Try it out!!
Put these sentences in conditional form.

When I finish my homework. I can get pizza.
When Elba behaves in class, she can get a cupcake.

                                               Inverse

Inverse is just adding not in the sentence to make it even with the conditional.

Example: If it is not raining then I do not need an umbrella.

Try It Out!!

Put the following statement in conditional and then in inverse form.

When I am hungry I eat pizza.

http://www.google.com/imgres?um=1&hl=en&biw=819&bih=316&tbm=isch&tbnid=jnKNLssFNkT_HM:&imgrefurl=http://pballew.blogspot.com/2010_10_01_archive.html&docid=FhR9DAHBzNanDM&imgurl=https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhJTapluXCf4RLyCcO4RFH6Mr2fShKgZw_V9WVsi_GWxofcBmsrdTx96tZl7dqqSb4VGPHkJUt9XQGFeHM3Mh1pkfuAhJXp1n0roaZL6OPN0uzsVumqi9wMBDz7VtigsbUCwGgtIlzRNSE/s1600/math-cartoon-10122009.gif&w=504&h=411&ei=yFtST76OLMXx0gGOnomeDw&zoom=1&iact=hc&vpx=134&vpy=-19&dur=13494&hovh=203&hovw=249&tx=155&ty=113&sig=114741552484678553676&page=1&tbnh=162&tbnw=199&start=0&ndsp=3&ved=1t:429,r:0,s:0

Aim: What is logic?

Logic in my eyes is common sense and thinking.

You have 18 marbles, you gave 5 to your friend Sam, 3 to Patrick, and 2 to Spongebob. How many marbles do you have left for your self?



All you need to do is use common sense you have eighteen marbles and you gave away 10.
How much do you have left?
Answer: You have eight left!!!




Question:

Mrs.Rosemarry has a garden full of flowers. She has 10 daisys, 10 roses, and 10 tulips. Mrs. Rosemarry wants Sandy to have at least one type from each flower. She has to pick them up
with out looking. How many does she need in order to have 1 flower from each type?

Answer: 21


http://www.google.com/imgres?um=1&hl=en&biw=819&bih=316&tbm=isch&tbnid=0v6dYxUHHt9FRM:&imgrefurl=http://www.flickriver.com/photos/bagdadcafe/tags/tulip/&docid=rCDv0BGck5rA9M&imgurl=http://farm1.static.flickr.com/193/450362635_5c8d789683.jpg&w=500&h=319&ei=yF1ST6H-EuT30gHf1OTTDQ&zoom=1&iact=hc&vpx=392&vpy=2&dur=1326&hovh=179&hovw=281&tx=185&ty=93&sig=114741552484678553676&page=2&tbnh=111&tbnw=148&start=3&ndsp=12&ved=1t:429,r:2,s:3