Aim:How do we use the other definitions of transformations?

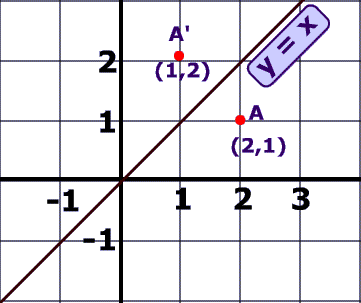
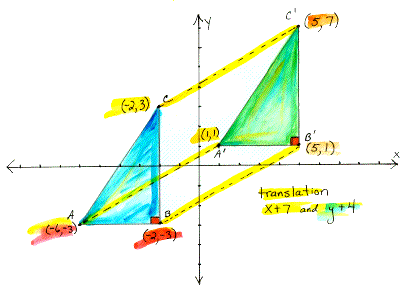Glide reflection
The combination of a reflection in a line and a translation along
 that line.

Orientation
Orientation refers to the arrangment of points relative to one another after a transformation
 has occured.

Isometry
An isometry is a transformation that preserves length.

A direct isometry preserves orientation.

Opposite isometry changes the order clockwise or counter clockwise.

Invariant
A figure  or property that remains unchanged under a transformation of the plane is
 referred to as invariant. Meaning no variations(changes) have occured.


Question

What is the vocabulary

word that means it  preserves the same length?

Aim: How do we review transformations?

There are four types of transformations. Reflection,translation,rotation,and dialation.
A translation "slides" an object a fixed distance in a given direction.  The original object and its translation have the same shape and size, and they face in the same direction.  A translation creates a figure that is congruent with the original figure and preserves distance (length) and orientation (lettering order).  A translation is a direct isometry.

Properties preserved (invariant) under a translation:1.  distance (lengths of segments are the same)
2.  angle measures (remain the same)
3.  parallelism (parallel lines remain parallel)
4.  colinearity (points stay on the same lines)
5.  midpoint (midpoints remain the same in each figure)
6.  orientation (lettering order remains the same)


Reflection: Figure is flipped over a line of symetry.
Properties preserved (invariant) under a line reflection:1.  distance (lengths of segments are the same)
2.  angle measures (remain the same)
3.  parallelism (parallel lines remain parallel)
4.  colinearity (points stay on the same lines)
5.  midpoint (midpoints remain the same in each figure)
------------------------------------------------------------------



Rotation: When a figure is turned around a single point.

Properties preserved (invariant) under a rotation:1.  distance is preserved (lengths of segments are the same)
2.  angle measures (remain the same)
3.  parallelism (parallel lines remain parallel)
4.  colinearity (points stay on the same lines)
5.  midpoint (midpoints remain the same in each figure)
6.  orientation (lettering order remains the same)

Rotation of 90°:
Rotation of 180°:	(same as point reflection in origin)
Rotation of 270°:

A dilation is a transformation (notation ) that produces an image that is the same shape as the original, but is a different size.   A dilation stretches or shrinks the original figure.    

Properties preserved (invariant) under a dilation:1.  angle measures (remain the same)
2.  parallelism (parallel lines remain parallel)
3.  colinearity (points stay on the same lines)
4.  midpoint (midpoints remain the same in each figure)5.  orientation (lettering order remains the same)
---------------------------------------------------------------
6.  distance is NOT preserved (NOT an isometry)
     (lengths of segments are NOT the same in all cases
      except a scale factor or 1.)

Question: What is the image of (5,6) after reflection on y-axis?

Transformations

Aim: How do we solve composition of transformation problems?

A composition transformation is when you perform 2 or more transformations.For instance reflection and then translation is called a glide reflection.

Always do the one with the circle first.



Given point A(-5,4). Determine the coordinates of A', the image of A under the composition T-5,4 r y-axis.

Reflect the points (-5,4) on the y-axis which means that the x changes to the opposite sign.
Therefore, (-5,4) becomes (5,4). Then you translate (5,4) five to the left and 4 to the right.
Your final answer is points (10,8).

Another problem would be  given point s(2,6). Determine the image of s prime after T-3,4 o r x-axis.
First you reflect point (2,6) on the x-axis . Which then the y changes to the opposite sign so the new point is (2,-6).
After, that you translate the point (2,-6) by subtracting 3 to the x and adding 4 to the y. S prime will be (-1,-2).


Question:
Given point H (3,5). Determine the image of H prime after reflection on y-axis and translation 6,-2.

Reflections

Aim: How do we solve problems using reflections?

Answer: You count the amount of square units from the point you are doing and reflect it over the x-axis  or y-axis.

Under a reflection the image is flipped over although the figure does not change in sizeor shape.

The reflection of the point (x, y) across the x-axis is the point (x, -y).

         Reminder: If you forget the rules for reflections when graphing, simply fold your graph paper along the line of reflection (in this example the x-axis) to see where your new figure will be located. 
As you can see when you reflect over the x-axis the y changes to the opposite sign.

When you reflect over the y-axis the x changes to the oppisite sign.

The reflection of the point (x, y) across the y-axis is the point (-x, y).    or

When you reflect a point across the line y = x, the x-coordinate and the y-coordinate change places.  When you reflect a point across the line y = -x, the x-coordinate and the y-coordinate change places and are negated (the signs are changed). 

 

The reflection of the point (x, y) across the line y = x  is the point (y, x).       or      The reflection of the point (x, y) across the line y = -x  is the point (-y, -x).    or

Questions

What is the image of the point (2,4) under the translation T-6,1?

Distance Formula

Aim: How do we write equations of circles?

When we need to find the length (distance) of a segment we simply COUNT the distance!

 When working with diagonal segments, use the Distance Formula to determine the length.


It doesn't matter which point you start with. Just start with the same point for reading both the x and y coordinates.

An example would be the following:





The Distance Formula is really just a coordinate geometry way of writing the Pythagorean Theorem. If you cannot remember the Distance Formula, you can always draw a graph and use the Pythagorean Theorem.

Transformations

Aim: how do we identify transformations?

Transformation: Transformation is when you move a geometric figure.

There are four types of transformation which are the following : translation, rotation, dialation, and reflection.

Translation : when every point is moved in the same direction as well as the same distance.

Reflection: Figure is flipped over a line of symetry.



Rotation: Figure is turned over around a single point.

 

Rotation of 90°:
Rotation of 180°:	(same as point reflection in origin)
Rotation of 270°:

Dialation: An enlargement or reduction in size of a figure.


        The reflection of the point (x,y) across the x-axis is the point (x-y)


<><><><> <><><><>

<>

The reflection of the point (x, y) across the y-axis is the point (-x, y). Questions: Coordinates (4,-6) what is the point after rotation of 180 ??? Answer: (-4,6)