Reflections

Aim: How do we solve problems using reflections?

Answer: You count the amount of square units from the point you are doing and reflect it over the x-axis  or y-axis.

Under a reflection the image is flipped over although the figure does not change in sizeor shape.

The reflection of the point (x, y) across the x-axis is the point (x, -y).

         Reminder: If you forget the rules for reflections when graphing, simply fold your graph paper along the line of reflection (in this example the x-axis) to see where your new figure will be located. 
As you can see when you reflect over the x-axis the y changes to the opposite sign.

When you reflect over the y-axis the x changes to the oppisite sign.

The reflection of the point (x, y) across the y-axis is the point (-x, y).    or

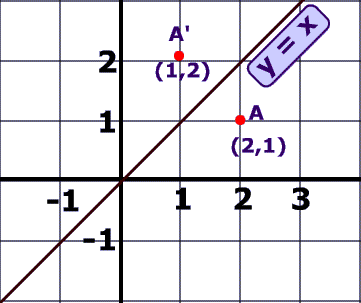
When you reflect a point across the line y = x, the x-coordinate and the y-coordinate change places.  When you reflect a point across the line y = -x, the x-coordinate and the y-coordinate change places and are negated (the signs are changed). 

 

The reflection of the point (x, y) across the line y = x  is the point (y, x).       or      The reflection of the point (x, y) across the line y = -x  is the point (-y, -x).    or

Questions

What is the image of the point (2,4) under the translation T-6,1?